So if a is an m n matrix then the product a x is defined for n 1 column vectors x.
2 x 1 column matrix.
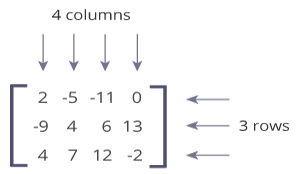
The number of rows is m and the number of columns is n.
The size or dimensions m n of a matrix identifies how many rows and columns a specific matrix has.
Let us define the multiplication between a matrix a and a vector x in which the number of columns in a equals the number of rows in x.
In mathematics a matrix plural matrices is a rectangular array or table see irregular matrix of numbers symbols or expressions arranged in rows and columns.
The dot product is performed for each row of a and each column of b until all combinations of the two are complete in order to find the value of the corresponding elements in matrix c.
A matrix is a rectangular arrangement or array of numbers often called elements.
A matrix this one has 2 rows and 3 columns to multiply a matrix by a single number is easy.
Provided that they have the same size each matrix has the same number of rows and the same.
For example when you perform the dot product of row 1 of a and column 1 of b the result will be c 1 1 of.
A 1 1 b 1 1 a 1 2 b 2 1 a 1 3 b 3 1 c 1 1.
The resulting matrix xβ has n rows and 1 column.
Note that the matrix multiplication ba is not possible.
A 2 4 extract the element in row 2 column 4 ans 8 more generally one or both of the row and column subscripts can be vectors.
For another example if x is an n k 1 matrix and β is a k 1 1 column vector then the matrix multiplication xβ is possible.
Similarly a row vector or row matrix is a 1 m matrix that is a matrix consisting of a single row of m elements.
Multiplying a matrix by another matrix.
Indicates that a is the m x n matrix whose i j entry is a ij.
The dimension of a matrix must be known to identify a specific element in the matrix.
That is c is a 2 5 matrix.
A 2 4 1 2 ans 5 11 9 7 4 14.
In linear algebra a column vector or column matrix is an m 1 matrix that is a matrix consisting of a single column of m elements.
Throughout boldface is used for the row and column vectors.
These are the calculations.
In general the i j entry of a matrix a is written a ij and the statement.
The transpose indicated by t of a row vector is a column vector.
For example the dimension of the matrix below is 2 3 read two by three because there are two rows and three columns.
The resulting matrix c ab has 2 rows and 5 columns.